Representation of low-precision models¶
The goal of this document is to describe how optimized models are represented in OpenVINO Intermediate Representation (IR) and provide guidance on interpretation rules for such models at runtime.
Currently, there are two groups of optimization methods that can influence on the IR after applying them to the full-precision model:
Sparsity. It is represented by zeros inside the weights and this is up to the hardware plugin how to interpret these zeros (use weights as is or apply special compression algorithms and sparse arithmetic). No additional mask is provided with the model.
Quantization. The rest of this document is dedicated to the representation of quantized models.
Representation of quantized models¶
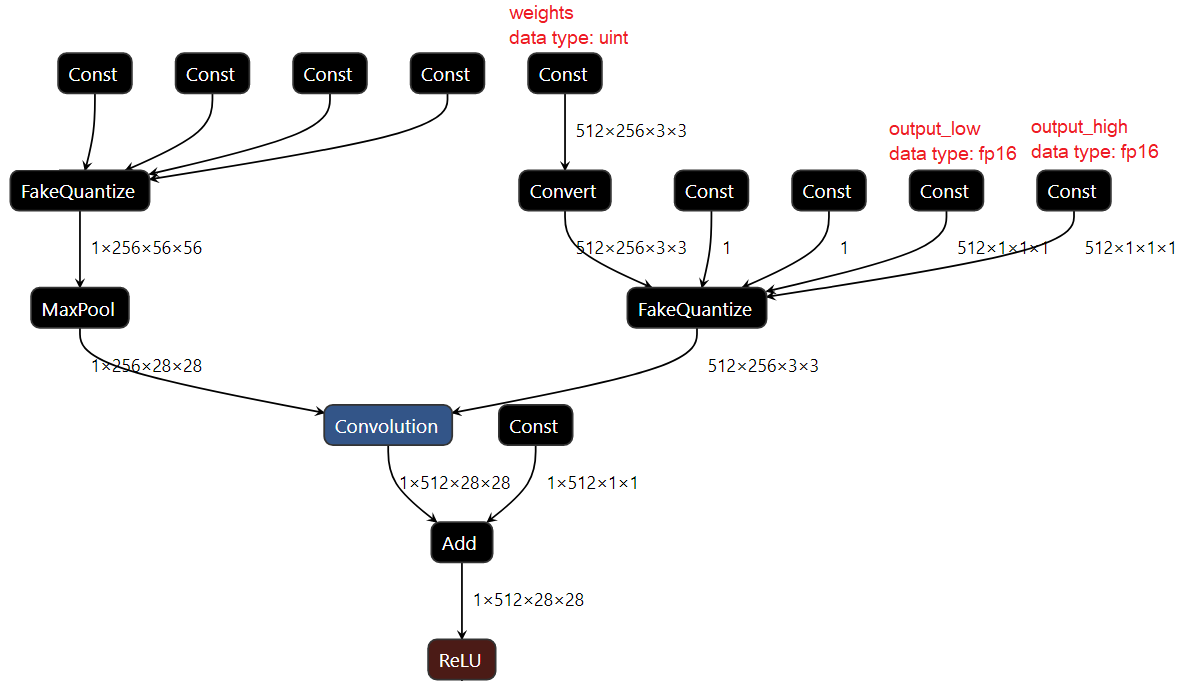
The OpenVINO Toolkit represents all the quantized models using the so-called FakeQuantize operation (see the description in this document). This operation is very expressive and allows mapping values from arbitrary input and output ranges. The whole idea behind that is quite simple: we project (discretize) the input values to the low-precision data type using affine transformation (with clamp and rounding) and then reproject discrete values back to the original range and data type. It can be considered as an emulation of the quantization process which happens at runtime. In order to be able to execute a particular DL operation in low-precision all its inputs should be quantized i.e. should have FakeQuantize between operation and data blobs. The figure below shows an example of quantized Convolution which contains two FakeQuantize nodes: one for weights and one for activations (bias is quantized using the same parameters).
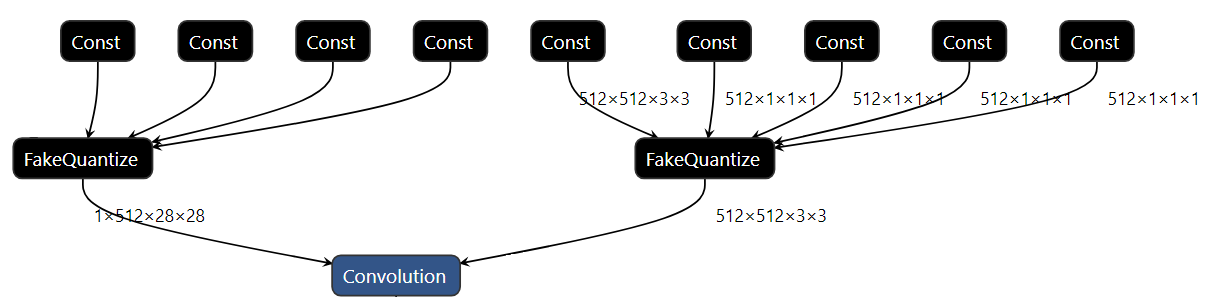
Starting from OpenVINO 2020.2 release all the quantized models are represented in the compressed form. It means that the weights of low-precision operations are converted into the target precision (e.g. INT8). It helps to substantially reduce the model size. The rest of the parameters can be represented in FLOAT32 or FLOAT16 precision depending on the input full-precision model used in the quantization process. Fig. 2 below shows an example of the part of the compressed IR.